Example for range sum query

I stumbled upon an interesting problem [1] a while ago:

--- Day 6: Probably a Fire Hazard ---
Because your neighbors keep defeating you in the holiday house decorating contest year after year,
you've decided to deploy one million lights in a 1000x1000 grid.
Furthermore, because you've been especially nice this year,
Santa has mailed you instructions on how to display the ideal lighting configuration.
Lights in your grid are numbered from 0 to 999 in each direction;
the lights at each corner are at 0,0, 0,999, 999,999, and 999,0.
The instructions include whether to turn on, turn off,
or toggle various inclusive ranges given as coordinate pairs.
Each coordinate pair represents opposite corners of a rectangle, inclusive;
a coordinate pair like 0,0 through 2,2 therefore refers to 9 lights in a 3x3 square.
The lights all start turned off.
To defeat your neighbors this year, all you have to do is set up your lights by doing
the instructions Santa sent you in order.
For example:
turn on 0,0 through 999,999 would turn on (or leave on) every light.
toggle 0,0 through 999,0 would toggle the first line of 1000 lights,
turning off the ones that were on, and turning on the ones that were off.
turn off 499,499 through 500,500 would turn off (or leave off) the middle four lights.
After following the instructions, how many lights are lit?
---

Auxiliary setup

To compare different approaches, 1000x1000 grid turns out to be too small. To spare myself of having to generate the test cases, I will:

use the input provided by AOC but randomly shuffled:
```
sort -R original_input.txt > shuffled_input.txt
```
introduce a coefficient k. The grid size becomes \( k \cdot 1000 \times k \cdot 1000 \) and each input coordinate is multiplied by k. Setting k=1 means solving the exact original problem.

Naive solution

The naive solution is to initialize the 1000x1000 grid, consume input and update the grid according to instructions and finally count how many grid cells are on.

A simple optimization can be done to maintain the numbers online, thus not needing to do the final grid walkthrough, but that would still leave the worst case runtime at O( \( R \times N^2 \) ) (R is a number of rectangles, N is the side of the grid).

Example run:


./target/release/bin 1 naive < src/input_shuffled.txt
211412

Optimized solution

One thing that struck me is we, human, can quickly compute the answer for the case when 2 huge rectangles overlap by 1:


turn on 0,0 through 500,500
turn on 500,500 through 999,999
turn off 0,0 through 500,500
toggle 500,500 through 999,999

Exapmle where humans can quickly compute the answer, no matter the size of the areas covered:

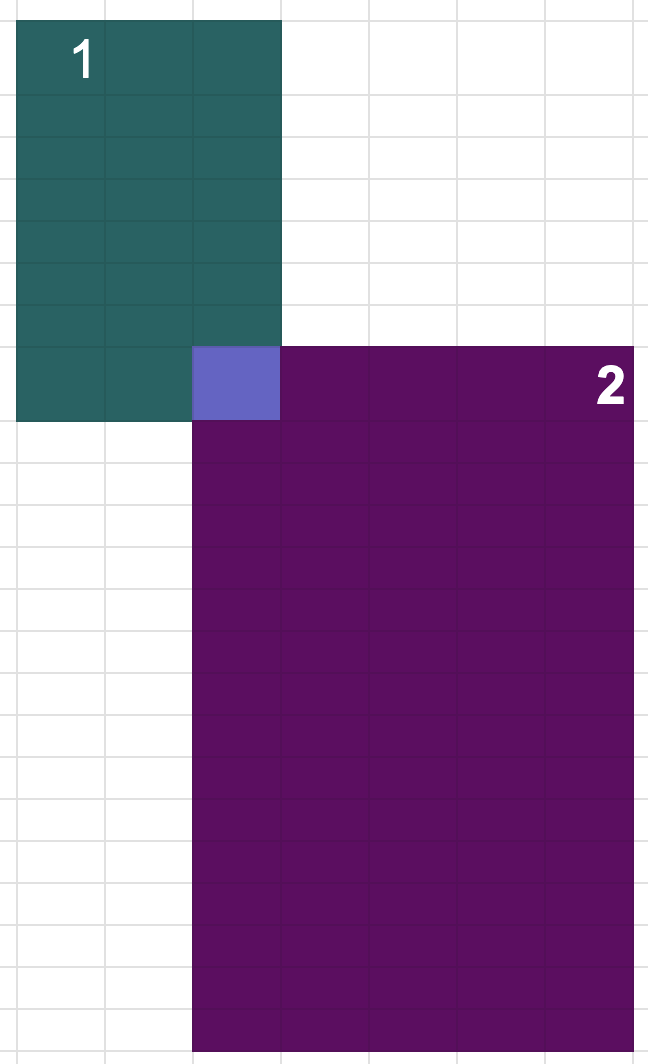
Note that running this with k=1, k=100, k=1000 should obviously produce the same result of 1 overlapping cell, and humans would be quick to realize that.

However, a naive solution would take progressively longer as we increase k.

The idea of an optimized approach is as follows. We can sweep a vertical line and maintain the set of rectangles that fall into the current horizontal segment.

Code 1: sweeping vertical line


for pair in events_by_x_coord.iter() {
    let x = pair.0;
    if let Some(x_prev_value) = x_prev {
        res += process_vertical_stripe(
            x_prev_value,
            *x,
            &active_set_within_vertical_stripe,
            &events_by_y_coord,
            z_index,
        );
    }
    for e in pair.1 {
        if e.is_open {
            active_set_within_vertical_stripe.insert(e.z_index);
        } else {
            active_set_within_vertical_stripe.remove(&e.z_index);
        }

        x_prev = Some(*pair.0);
    }
}

For a given horizontal segment, we can then sweep another - horizontal - line upwards and maintain a set of rectangles in the current vertical segment. While doing that we can check whether the rectangle is in the horizontal segment, that way having an exact set of rectangles that are present in the current rectangular patch.

Code 2: sweeping horizontal line


for p in events_by_y_coord.iter() {
    let y = p.0;
    if let Some(y_prev_val) = y_prev {
        if !active_set_within_horizontal_stripe.is_empty() {
            res += process_patch(
                x_prev_val,
                x,
                y_prev_val,
                *y,
                &active_on_within_horizontal_stripe,
                &active_off_within_horizontal_stripe,
                &fw_toggle,
                total_rectangles,
            );
        }
    }

    y_prev = Some(*y);

    for e in p.1.iter() {
        if !active_set_within_vertical_stripe.contains(&e.z_index) {
            continue;
        }

        match e.is_open {
            true => {
                active_set_within_horizontal_stripe.insert(e.z_index);
                match e.operation {
                    Operation::On => {
                        active_on_within_horizontal_stripe.insert(e.z_index);
                    }
                    Operation::Off => {
                        active_off_within_horizontal_stripe.insert(e.z_index);
                    }
                    Operation::Toggle => {
                        active_toggle_within_horizontal_stripe.insert(e.z_index);
                        fw_toggle.inc(e.z_index as usize);
                    }
                }
            }
            false => {
                active_set_within_horizontal_stripe.remove(&e.z_index);
                match e.operation {
                    Operation::On => {
                        active_on_within_horizontal_stripe.remove(&e.z_index);
                    }
                    Operation::Off => {
                        active_off_within_horizontal_stripe.remove(&e.z_index);
                    }
                    Operation::Toggle => {
                        active_toggle_within_horizontal_stripe.remove(&e.z_index);
                        fw_toggle.dec(e.z_index as usize);
                    }
                }
            }
        }
    }
}

The next question is how to process a separate patch. The basic idea is this: any sequence of "on", "off" and "toggle" is equivalent to "on" or "off" followed by some numbers of toggles.

For example, 1:"on", 2:"off", 3:"off", 4:"on", 5:"toggle", 6:"on", 7:"toggle" is equivalent to just 6:"on", 7:"toggle" because the "on" at step 6 makes it irrelevant what was the prior sequence.

To quickly compute number of toggles that happened after a certain index, we can employ range some query.

Code 3: figuring out the state of the patch


fn process_patch(
    left: u32,
    right: u32,
    bottom: u32,
    top: u32,
    turn_on: &BTreeSet,
    turn_off: &BTreeSet,
    fw_toggle_active: &FenwickTree,
    total_rectangles: i32,
) -> u32 {
    let mut base_val = false;
    let mut last_turn: i32 = *turn_off.last().unwrap_or(&-1);
    if let Some(turn_on_last) = turn_on.last() {
        if *turn_on_last > last_turn {
            last_turn = *turn_on_last;
            base_val = true;
        }
    }

    let toggles_after_last_turn = fw_toggle_active.sum_range(last_turn + 1, total_rectangles - 1);
    if toggles_after_last_turn % 2 == 1 {
        base_val = !base_val;
    }

    if base_val {
        let h = (right - left) as u32;
        let v = (top - bottom) as u32;
        h * v
    } else {
        0
    }
}

So we need to maintain the sorted set of "on" and "off" rectangles to quickly identify the last "on" or "off". After that we need to know how many toggles happened thereafter - range sum query would work, and one way to do it efficiently is via fenwick tree. Finally, when we know the last action ("on" or "off") and how many toggles happened afterwards, we can compute the state of the whole patch (either "on" or "off). And knowing the area of the patch we can then add it to the final result.

In this example we have 3 rectangles: 1, 2, 3. We have 5 segments between vertical lines: V1, V2, ..., V5. We have 5 segments between horizontal lines: H1, H2, ... H5.

Runtime analysis

To pre-process input: \( R \log R \) since we read R rectangles and add data to sets and maps.

To compute result:

O(\( R \log R \)) to sweep vertical line
O(\( R \log R \)) to sweep horizontal line
O(\( \log R \)) to perform range sum query

Giving O(\( R^2 \log^3 R \))

Note that it doesn't depend on the size of the grid or of any of the retangles anymore, but only on the number of rectangles.

Fenwick tree implementation

See [2] for the original C++ code.
See [7] for the adopted Rust implementation based on above.


pub struct FenwickTree {
    size: usize,
    t: Vec,
}

impl FenwickTree {
    pub fn new(n: usize) -> FenwickTree {
        FenwickTree {
            size: n,
            t: vec![0; n as usize],
        }
    }

    pub fn sum(&self, mut range: i32) -> u32 {
        let mut res: u32 = 0;
        while range >= 0 {
            res += self.t[range as usize];
            range = (range & (range + 1)) - 1;
        }
        res
    }

    pub fn inc(&mut self, mut i: usize) {
        while i < self.size {
            self.t[i] += 1;
            i = i | (i + 1);
        }
    }

    pub fn dec(&mut self, mut i: usize) {
        while i < self.size {
            self.t[i] -= 1;
            i = i | (i + 1);
        }
    }

    pub fn sum_range(&self, l: i32, r: i32) -> u32 {
        self.sum(r) - self.sum(l - 1)
    }
}

Experiments

The data below has been collected by running the command:


% /usr/bin/time -lh ./target/release/bin 10 naive < src/input_shuffled.txt
20992232
Time: 2431 ms
	2.43s real		2.41s user		0.01s sys
           104857600  maximum resident set size
                   0  average shared memory size
                   0  average unshared data size
                   0  average unshared stack size
                6583  page reclaims
                  13  page faults
                   0  swaps
                   0  block input operations
                   0  block output operations
                   0  messages sent
                   0  messages received
                   0  signals received
                   4  voluntary context switches
                  28  involuntary context switches
         51317968081  instructions retired
          9501259555  cycles elapsed
           104596544  peak memory footprint

% /usr/bin/time -lh ./target/release/bin 10 optimized < src/input_shuffled.txt
20992232
Time: 20 ms
	0.02s real		0.02s user		0.00s sys
             1769472  maximum resident set size
                   0  average shared memory size
                   0  average unshared data size
                   0  average unshared stack size
                 303  page reclaims
                   0  page faults
                   0  swaps
                   0  block input operations
                   0  block output operations
                   0  messages sent
                   0  messages received
                   0  signals received
                   0  voluntary context switches
                  13  involuntary context switches
           119355746  instructions retired
            51174896  cycles elapsed
             1426240  peak memory footprint

The lines above would be producing data points:

        k=10: naive time 2431 ms, naive memory 99.8 Mb
        k=10: optimized time 20 ms, optimized memory 1.4 Mb

Time Comparison (ms)

Memory Comparison (MB)

Full code and references

[1] The original problem is taken from here: https://adventofcode.com/2015/day/6

[2] The fenwick tree implementation is a rip-off of this: http://e-maxx.ru/algo/fenwick_tree

[3] Full source code directory: link

[4] Test file input_shuffled.txt

[5] Test file easy_for_humans.txt

[6] Full code of main.rs

[7] Full code of fw.rs

Back to main page